Low-rank approximation 1/4
Low-rank approximation
Low-rank approximation is a technique used to simplify complex data by approximating it with a smaller or “lower-rank” version while keeping the important information. It’s like compressing data, but without losing the essential patterns or structure.
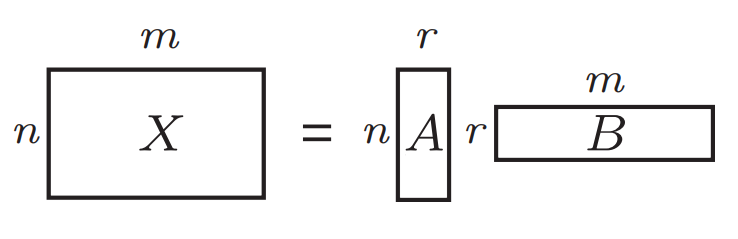
Matrix Representation: In math, data can often be represented as a matrix (a grid of numbers). For example, if you have a large dataset, it might be represented by a matrix with many rows and columns. The “rank” of this matrix refers to the number of linearly independent rows or columns—basically, how complex the data is.
Low-Rank Approximation: Instead of using the entire matrix, low-rank approximation tries to find a smaller matrix that captures the same important features of the original one. You can think of this smaller matrix as a “compressed” version that focuses on the key relationships in the data, ignoring the less important details (like noise or redundancy).
Why do we use it?
we have dsd
Faster Computation: Instead of directly multiplying large matrices, low-rank approximation allows us to work with smaller matrices, which speeds up computation. The time complexity can reduce from \(O(nm)\) to \(O((n+m)r)\), where r is the rank of the approximation.
Efficiency: Large datasets or images require a lot of memory and computational power. By using low-rank approximation, you can reduce the amount of data you need to work with while still keeping the important information.
Data Compression: It helps compress the data, making it easier to store and transmit.
Noise Reduction: In real-world data, there’s often noise (unnecessary or irrelevant information). Low-rank approximation can help filter out this noise and keep the meaningful structure.
Low-rank approximation Techniques
Low-rank approximation techniques are methods used to approximate a large, complex matrix with a smaller matrix that has lower rank, meaning it captures the most important information while reducing redundancy and noise. Here are the most common techniques used for low-rank approximation, along with their advantages and disadvantages:
1. Singular Value Decomposition (SVD)
Singular Value Decomposition is one of the most commonly used techniques for low-rank approximation. It decomposes a matrix \(A\) into three components:
\[ A = U \Sigma V^T \]
Where:
\(U\) and \(V\) are orthogonal matrices,
\(\Sigma\) is a diagonal matrix containing the singular values (which represent the importance of different components).
You can then select the top \(k\) singular values and their corresponding vectors to create a low-rank approximation.
Advantages:
- Optimal Approximation: SVD provides the best low-rank approximation in terms of minimizing the error (Frobenius norm or 2-norm).
- Widely Used: SVD is robust and well-understood, making it a standard technique in fields like machine learning, data compression, and image processing.
- Noise Filtering: SVD automatically filters out the “noise” (small singular values) when approximating, keeping the dominant trends.
Disadvantages:
- Computationally Expensive: Computing SVD for large matrices can be slow and requires a lot of memory, especially for big data applications.
- Global Information: SVD captures global structure but might miss fine, local patterns in data (like small clusters in a dataset).
2. Principal Component Analysis (PCA)
PCA is essentially a variation of SVD applied to the covariance matrix. It identifies the directions (principal components) where the variance in the data is the largest, and projects the data onto those directions. This allows you to represent the data using fewer dimensions while retaining the most important patterns.
Advantages:
- Dimensionality Reduction: PCA is ideal for reducing the dimensionality of data while keeping the key patterns, which makes it easier to visualize or process.
- Efficient for Small Datasets: PCA works well on relatively small datasets and is fast for low-rank approximations in these cases.
- Noise Reduction: Like SVD, it helps in removing noise and focusing on the key features.
Disadvantages:
- Linear Assumptions: PCA assumes that the important relationships in the data are linear, which may not be the case for more complex, non-linear datasets.
- Sensitive to Scaling: PCA is sensitive to how the data is scaled. You need to normalize or standardize the data for the best results.
- Loss of Interpretability: The new principal components are linear combinations of the original features, which can make the results hard to interpret.
3. Non-negative Matrix Factorization (NMF)
NMF is a technique used for matrices where all values are non-negative. It decomposes the matrix into two smaller non-negative matrices \(W\) and \(H\):
\[ A \approx WH \]
The idea is to represent the original matrix as a combination of “basis vectors” in \(W\) and “coefficients” in \(H\), both constrained to be non-negative, which can be helpful when dealing with data that naturally contains non-negative values (like images or word counts).
Advantages:
- Interpretability: Since both the basis vectors and coefficients are non-negative, the results are often easier to interpret. For example, in image processing, NMF will break down an image into parts that represent things like edges, textures, etc.
- Sparsity: NMF often produces sparse solutions, meaning that many of the elements in \(W\) and \(H\) are zero, which can make the results more efficient and interpretable.
Disadvantages:
- Not Globally Optimal: Unlike SVD, NMF does not guarantee an optimal approximation. It may get stuck in local minima during the optimization process.
- Computational Complexity: While it can be faster than SVD in some cases, NMF is still computationally expensive for large datasets, especially due to its iterative optimization process.
4. QR Decomposition
QR decomposition breaks down a matrix \(A\) into two matrices \(Q\) (orthogonal matrix) and \(R\) (upper triangular matrix). For low-rank approximation, the matrix can be reduced to its top \(k\) components by selecting a subset of columns from \(Q\) and rows from \(R\).
Advantages:
- Efficient for Solving Systems: QR decomposition is particularly efficient for solving linear systems and least-squares problems, especially when combined with column-pivoting.
- Numerical Stability: It is often numerically more stable than other techniques like Gaussian elimination.
Disadvantages:
- Not the Best for Low-Rank Approximation: QR decomposition is not specifically designed for low-rank approximation, so it doesn’t minimize approximation error as effectively as SVD.
- Interpretation: While it’s fast, QR decomposition is less interpretable compared to SVD or NMF, which can give a clearer sense of what the reduced components represent.
5. Randomized Low-Rank Approximation
Randomized algorithms approximate low-rank decompositions by using random projections to quickly identify the most important components of the matrix. The idea is to approximate the original matrix with random sampling and then refine the approximation using techniques like SVD.
Advantages:
- Speed: Randomized algorithms are much faster than traditional methods like SVD, making them ideal for very large datasets (like big data or streaming data).
- Scalability: Because they are faster, randomized algorithms are more scalable to huge datasets.
Disadvantages:
- Approximation Error: Randomized methods introduce some additional approximation error compared to traditional techniques like SVD. The trade-off is between speed and accuracy.
- Uncertainty: The randomization aspect can lead to different results each time the algorithm runs, making the results somewhat non-deterministic.
6. CUR Decomposition
CUR decomposition is a matrix approximation technique that selects actual rows and columns from the original matrix to form two low-rank matrices \(C\) (columns) and \(R\) (rows). The matrix \(U\) is constructed by relating the selected rows and columns.
Advantages:
- Interpretability: Since CUR selects actual rows and columns from the original matrix, the results are more interpretable than SVD, which gives linear combinations.
- Sparsity: CUR often results in sparse representations that can be computationally efficient and easier to store.
Disadvantages:
- Less Accurate: It tends to be less accurate than SVD for minimizing approximation error.
- Complexity: While it has some advantages in specific cases, CUR is more complex to implement and may not work well for all types of data.
Summary Table
| Technique | Advantages | Disadvantages |
|---|---|---|
| SVD | Best approximation, noise filtering | Computationally expensive |
| PCA | Dimensionality reduction, fast for small data | Assumes linearity, sensitive to scaling |
| NMF | Interpretability, good for non-negative data | Can get stuck in local minima, computational cost |
| QR Decomposition | Efficient for solving systems | Not ideal for low-rank approximations |
| Randomized | Fast, scalable | Introduces approximation error |
| CUR | Interpretability, actual rows and columns | Less accurate than SVD, complex |
In conclusion, the choice of low-rank approximation technique depends on the specific problem you’re solving. If you need the most accurate approximation and don’t mind computational cost, SVD or PCA are good choices. For non-negative data or interpretability, NMF and CUR are useful, while randomized methods excel when speed is critical.
Among the low-rank approximation techniques discussed, Randomized Low-Rank Approximation is typically the fastest method, especially for very large datasets.
Why Randomized Low-Rank Approximation is Fast:
Random Sampling: Instead of analyzing the entire matrix directly (as in SVD or PCA), randomized methods first perform a random sampling or projection of the data to a lower-dimensional space. This drastically reduces the computational workload right from the start.
Dimensionality Reduction Early: By quickly approximating the matrix structure through random projections, the method avoids performing computations on the full matrix, which saves time.
Scalability: It scales efficiently with large datasets, making it suitable for scenarios where traditional methods like SVD would take too long (for example, in big data applications).
Speed Comparison with Other Methods:
SVD/PCA: These are slower because they require calculating the full decomposition of the matrix. SVD, in particular, is computationally expensive, with a time complexity of \(O(mn^2)\) for an \(m \times n\) matrix.
NMF: NMF is slower than randomized algorithms because it involves iterative optimization that can take time to converge.
QR Decomposition: QR can be faster than SVD but isn’t primarily designed for low-rank approximation, and for large datasets, randomized methods will still outperform QR.
CUR: CUR is not optimized for speed, as it involves selecting actual rows and columns and then performing further matrix operations, which can be slow for large matrices.
Trade-offs:
- Randomized Low-Rank Approximation is fast but may introduce some approximation error compared to more precise methods like SVD. The trade-off here is between speed and accuracy.
- However, for very large datasets or situations where speed is critical (like real-time processing or working with big data), randomized methods strike a good balance between performance and quality.
In summary, randomized low-rank approximation is generally the fastest technique, especially when working with large-scale matrices or datasets.